Computer Graphics MCS 053
Q Write Midpoint Circle Generation Algorithm. Computer coordinate points of circle drawn with centre at (0,0) and radius 5, using midpoint circle algorithm.
Solution: Ref link
Q Discuss the Taxonomy of projection with suitable diagram. How Perspective projection differs from Parallel projection. Derive a transformation matrix for a perspective projection of a point P (x,y,z) onto a x=4 plane as viewed from E (6, 0, 0)
Solution Ref link
Q Write Bresenham line drawing algorithm and DDA algorithm? Compare both algorithms and identify which one is better and why? Draw a line segment joining (4, 8) and (8, 10) using both algorithms i.e. Bresenham line drawing algorithm and DDA algorithm.
Solution Ref link
Q What is Bezier Curve? Discuss the Role of Bernstein Polynomial in
Bezier Curve. How Bezier curves contribute to Bezier Surfaces? Prove the following properties of Bezier curve.
(i) P(u=1) = Pn (ii) P’(0) = n (P1-P0)
Given four control points PO (2, 2) P1 (3, 4) P2 (5, 4) and P3 (4,2) as vertices of Bezier curve. Determine four points of Bezier Curve.
Solution Ref link
Q What is the advantage of using homogenous co-ordinate system over
Euclidean coordinate sstem? Consider the square ABCD with vertices A(0, 0),B (0, 2),C (2, 0), D (2, 2). Perform a composite transformation of the square by performing the following steps. (Give the coordinates of the square at each steps).
(i) Scale by using 𝑆x=2 and 𝑆y = 3
(ii) Rotate of 450 in the anticlockwise direction
(iii) Translate by using 𝑇x = 3 and 𝑇y = 5
Solution Ref link
Q Derive the 2D-transformtion matrix for reflection about the line y=mx, where m is a constant. Use this transformation matrix to reflect the triangle A (0,0) ,B(1, 1), C(2 ,0) about the line y=2x.
Solution Ref link
Q Explain the scan line polygon filling algorithm with the help of suitable diagram.
Ans scan-line algorithm scopes for the intersection points of the scanline with each edge of the area to be filled. It scans from left to right, identifying pair of intersections and pixels with specific color intensity. Even number of pixel correspond to interior of polygon whereas odd number intersection do not correlate with interior of polygon. This algorithm works by intersecting scanline with polygon edges and fills the polygon between pairs of intersections. The following steps depict how this algorithm works.
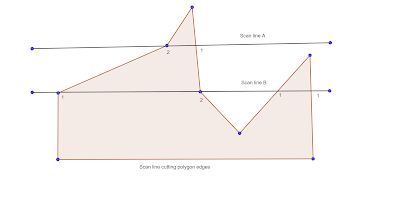
Ref diagram, scanline B intersects five polygon edges whereas scanline A intersects four polygon edges. But there is a difference. For scanline B, the two intersecting edges sharing a vertex are an opposite side of the scanline but for scanline A, the two intersecting edges are both above the scan line. In scanline B,extra processing
would be required. One intersection point is stored if two intersecting edges sharing a vertex are opposite to scanline else two intersection points are stored.
Step 1. Sort the polygon sides on the largest y-value.
Step 2. Start with largest y-value and scan down the polygon.
Step 3. For each y, determine which sides can be intersected and find the x values of these intersection point.
Step 4. Sort, pair and pass the x- values of the line drawing routine
Q What is the role of light in computer graphics?
Ans In order to generate visibility the presence of light is one of the basic requirements. It is obvious that without light and the interaction of light with objects, we would never see anything at all. A study of the properties of light and how light interacts with the surfaces of objects is hence vital in producing realistic images in Computer Graphics.
So before considering the production of images to be used in animation or any other application it is worth studying some of the basic properties of light and colour and also to introduce the modeling of the interaction of light with surfaces in Computer Graphics because attainment of realism is one of the basic motives of computer graphics and without considering the effect of light the same cannot be achieved.
Q Discuss the lamberts cosine law?
Ans Lambert's cosine law: “LAMBERTS COSINE LAW” states that the radiant energy from any small surface area dA in any direction θ relative to the surface normal is proportional to Cos θ. In case of diffused reflection the source is directional but reflection is uniform. Say, Id → Intensity of incident diffused light. Then as per the Lambert’s law the intensity of reflected light (I) will be α cos θ. Where, θ = Angle between unit direction of incident light vector and unit normal to the surface (or angle of incidence).
|
I = Kd Id cos θ
Kd → diffused reflection coefficient.
0 ≤ Kd ≤ 1
I= Kd Id (N.L)
I α cos θ ⇒ less θ leads to more reflection &more θ leads to less reflection
cos θ = cos θ (Q| N|&| L | are)
|
An important consequence of Lambert's cosine law is that when an area element on the surface is viewed from any angle, it has the same apparent brightness. This is because although the emitted intensity from an area element is reduced by the cosine of the emission angle, the observed size (solid angle) of the area element is also reduced by that same amount, so that while the area element appears smaller, its brightness is the same. For example, in the visible spectrum, the Sun is almost a Lambertian radiator, and as a result the brightness of the Sun is almost the same everywhere on an image of the solar disk. Also, a perfect black body is a perfect Lambertian radiator.
Q Explained ambient, diffused and specular reflection. Give general mathematical expression of each.
Ans The light intensity Ia of the ambient light source is distributed constantly throughout the scene. • The reflected ambient light I at a surface point can be written as I = ka · Ia where ka is the ambient reflection coefficient. • The ambient reflection coefficient is a constant out of the range [0,1]. • It represents the material property of the illuminated object.
As ambient lighting is not directed, uni-colored and uni-material objects still appear in one color. • Still, only the silhouettes can be perceived. • The color of the object depends on the amount of reflected light defined by the reflection coefficient.
This term is called the ambient reflection term and is modeled by a constant term. Again the amount of ambient light reflected is dependent on the properties of the surface.It is to be noted that if Ia → intensity of ambient light; Ka → property of material (Ambient reflection coefficient ka , 0 < ka < 1) then resulting reflected light is a constant for each surface independent of viewing direction and spatial orientation of surface.
Say, Ia → Intensity of ambient light.
I → Intensity of reflected ambient light
It is assumed that Ia ≠ 0 (Q Ia = 0 ⇒ These does not exit any light)
I α Ia ⇒ I = Ka Ia ; Ka → constant ; 0 ≤ Ka ≤ 1
Ka = 0 ⇒ object has absorbed the whole incident light.
Ka = 1 ⇒ object has reflected the whole incident light.
0 ≤Ka ≤1 ⇒ object has reflected some and absorbed some light.
Lambert‘s law: The reflected light intensity I at a point p on a surface is proportional to cos θ, where θ is the angle between the vector l pointing from p to the light source and the surface normal n in point p.
The reflected diffuse light I at a surface point p is given by I = IP · kd · cos θ = IP · kd · (n•l) where IP is the intensity of the diffuse light source and kd is the diffuse reflection coefficient (and assuming that l is normalized). • The diffuse reflection coefficient is a constant out of the range [0,1] and represents the material property of the illuminated object.
This model assumes that the light source sends out directed light and is of infinitely small extent (point light source). • Obviously, I=0 if n•l < 0. Taking this into account, we should write: I = IP · kd · max(n•l,0)
Attenuation: • Light intensity that spreads from a light source with finite extent decreases with increasing distance rP to the light source. • We need to add an attenuation factor fatt(rP). • We obtain: I = IP · kd · fatt(rP) · max(n•l,0). • Physical law: fatt(rP) ~ 1/rP2. • In practice, we use: fatt(rP) = min (1/(c0 + c1 · rP+ c2 · rP2),1) with real constants c0 , c1 , and c2.
The combined effect of ambient and diffused reflection is given by
I = Ia Ka + Id Kd cos θ = Ia Ka + Id Kd (N. L)
Specular reflection models reflection at shiny surfaces
It adds highlights to the illumination.
Phong‘s specular reflection model is based on perfect mirror reflection of light rays: r: direction of reflection rule: α = β Specular reflection depends on viewpoint: Specular reflection is highest, if viewpoint is in direction r
illumination = Ambient + Diffuse + Specular
A framebuffer is a portion of RAM containing a bitmap that drives a video display. It is a memory buffer containing a complete frame of data. Modern video cards contain frame buffer circuitry in their cores. This circuitry converts an in-memory bitmap into a video signal that can be displayed on a computer monitor. The Frame Buffer which is also called the Refresh Buffer or Bitmap. It is the refresh storage area in the digital memory, in which the matrix (array) of intensity values and other parameters (called attributes) of all the pixels making up the image are stored in binary form.In a Raster Scan System, the Frame buffer stores the picture information, which is the bit plane (with m rows and n columns).
The storage area in a raster scan display system is arranged as a two-dimensional table. Every row-column entry stores information such as brightness and/or colour value of the corresponding pixel on the screen. In a frame buffer each pixel can be represented by 1 to 24 or more bits depending on the quality (resolution) of the display system and certain attributes of the pixel. Higher the resolution, better the quality of the pictures. Commands to plot a point or line are converted into intensity and colour values of the pixel array or bitmap of an image by a process called Scan Conversion.
The display system cycles through the refresh buffer, row-by-row at speeds of 30 or 60 times per second to produce the image on the display. The intensity values picked up from the frame buffer are routed to the Digital/Analog converter which produces the necessary deflection signals to generate the raster scan. A flicker free image is produced by interlacing all odd-numbered scan lines that are displayed first from, top to bottom and then, all even-numbered scan lines that are displayed. The effective refresh rate to produce the picture becomes much greater than 30 Hz.
Q How frame buffer is different from the display buffer?
The Display buffer in Random Scan System, stores the picture information. Further, the device is capable of producing pictures made up of lines but not of curves. Thus, it is also known as “Vector display device or Line display device or Calligraphic display device”.
2) In a Raster Scan System, the Frame buffer stores the picture information, which is the bit plane (with m rows and n columns).Because of this type of storage the system is capable of producing realistic images, but the limitation is that, the line segments may not appear to be smooth.
Q How a frame buffer is used for putting colour and controlling intensity of any display device?
Framebuffers have traditionally supported a wide variety of color modes. Due to the expense of memory, most early framebuffers used 1-bit (2-color), 2-bit (4-color), 4-bit (16-color) or 8-bit (256-color) color depths. The problem with such small color depths is that a full range of colors cannot be produced. The solution to this problem was indexed color which adds a lookup table to the framebuffer. Each color stored in framebuffer memory acts as a color index. The lookup table serves as a palette with a limited number of different colors.
In some designs it was also possible to write data to the LUT (or switch between existing palettes) on the run, allowing dividing the picture into horizontal bars with their own palette and thus render an image that had a far wider palette. For example, viewing an outdoor shot photograph, the picture could be divided into four bars, the top one with emphasis on sky tones, the next with foliage tones, the next with skin and clothing tones, and the bottom one with ground colors. This required each palette to have overlapping colors, but carefully done, allowed great flexibility.
Q Why shading is required in computer graphics? Briefly discuss the role of interpolation technique in shading.
Ans: We need shading as during transformation of the 3D image into a 2D image there is a possibility of loss of information like depth, height, etc., of an object in the scene. So to preserve this we take different Illumination models into consideration, for preserving the information embedded in 3D scene & let it not be lost while transforming it in to 2D scene.
Role of interpolation technique in shading: Here polygon is rendered by linearly interpolating intensity values across the surface. Intensity values for each polygon are matched with the values of adjacent polygons along the common edges, thus eliminating the intensity discontinuities that can occur in flat shading.Calculations to be performed for each polygon surface rendered with Gourand shading:
1) Determine average unit normal vector at each polygon vertex.
2) Apply illumination model to each vertex to calculate the vertex intensity.
3) Linearly interpolate the vertex intensities over the surface of the polygon)
To determine average unit normal vector at each polygon vertex:
At each polygon vertex (as shown by point V in the figure), the normal vector is
obtained by averaging the surface normal of all polygons sharing that vertex. Thus, for
any vertex V the unit vertex normal will be given by Nv
K → 1 to n are the surfaces in contact with the vertex v.
Q Compare intensity interpolation and normal interpolation? Which interpolation technique contributes to which type of shading?
Ans Intensity interpolation is also known as Gourand Shading: It removes the intensity discontinuities associated with the constant shading model. Deficiencies: Linear intensity interpolation can cause bright and dark streaks called Mach bands to appear on the surface, these mach bands can be removed by using Phong shading or by dividing the surface into greater number of polygon faces. Note: In Gourand Shading because of the consideration of average normal, the intensity is uniform across the edge between two vertices. So on comparison both of interpolation techniques have some pros and cons.
Q Which Shading technique is better Phong shading or Gourand shading, Why?
Ans In Gouraud shading we were doing direct interpolation of intensities but a more accurate method for rendering a polygon surface is to interpolate normal vectors and then apply illumination model to each surface. This accurate method was given by Phong and it leads to Phong shading on Normal vector interpolation shading.
Q Write Z-buffer algorithm for hidden surface detection. Explain how this algorithm applied to determine the hidden surfaces.
Ans In z-buffer algorithm every pixel position on the projection plane is considered for determining the visibility of surfaces w. r. t. this pixel. On the other hand in scan-line method all surfaces intersected by a scan line are examined for visibility. The visibility test in z-buffer method involves the comparison of depths of surfaces w. r. t. a pixel on the projection plane. The surface closest to the pixel position is considered visible. The visibility test in scan-line method compares depth calculations for each overlapping surface to determine which surface is nearest to the view-plane so that it is declared as visible.
The process of identifying and removal of these hidden surfaces is called the visible-line or visible-surface determination, or hidden-line or hidden-surface elimination.
There are two fundamental approaches for visible-surface determination, according to whether they deal with their projected images or with object definitions directly. These two approaches are called image-space approach and object-space approach, respectively. Object space methods are implemented in the physical coordinate system in which objects are defined whereas image space methods are implemented in screen coordinate system in which the objects are viewed. In both cases, we can think of each object as comprising one or more polygons (or more complex surfaces). The first approach (image-space) determines which of n objects in the scene is visible at each pixel in the image. The pseudocode for this approach looks like as:
for(each pixel in the image)
determine the object closest to the viewer that is passed by the projector
draw the pixel in the appropriate color;
This approach requires examining all the objects in the scene to determine which is closest to the viewer along the projector passing through the pixel. That is, in an image-space algorithm, the visibility is decided point by point at each pixel position on the projection plane. If the number of objects is ‘n’ and the pixels is ‘p’ then effort is proportional to n.p.
The second approach (object-space) compares all objects directly with each other within the scene definition and eliminates those objects or portion of objects that are not visible. In terms of pseudocode, we have:
for (each object in the world)
determine those parts of the object whose view is unobstructed (not blocked)
parts of it or any other object;
draw those parts in the appropriate color;
}Z-buffer method, detects the visible surfaces by comparing surface depths (z-values) at each pixel position on the projection plane. In Scan-line method, all polygon surfaces intersecting the scan-line are examined to determine which surfaces are visible on the basis of depth calculations from the view plane. For scenes with more than one thousand polygon surfaces, Z-buffer method is the best choice.
Q What is animation? How it is different from Graphics?
The word Animation is derived from ‘animate’ which literally means ‘to give life to’, ‘Animating’ a thing means to impart movement to something which can’t move on its own. It is a time based phenomenon for imparting visual changes in any scene according to any time sequence, the visual changes could be incorporated through translation of object, scaling of object, or change in colour, transparency, surface texture etc.
Here, lies the basic difference between Animation and graphics. The difference is that animation adds to graphics, the dimension of time, which vastly increases the amount of information to be transmitted, so some methods are used to handle this vast information and these methods are known as animation methods down below is broad description of methods of animation combined into a film.
Second method: Here, the physical models are positioned to the image to be recorded. On completion the model moves to the next image for recording and this process is continued. Thus, the historical approach of animation has classified computer animation into two main categories:
- a) Computer-assisted animation usually refers to 2D systems that computerise the traditional animation process. Here, the technique used is interpolation between key shapes which is the only algorithmic use of the computer in the production of this type of animation equation, curve morphing (key frames, interpolation, velocity control), image morphing.
- b) Computer generated animation is the animation presented via film or video, which is again based on the concept of persistence of vision because the eye-brain assembles a sequence of images and interprets them as a continuous movement and if the rate of change of pictures is quite fast then it induce the sensation of continuous motion.
Low level techniques (motion specific)
Techniques used to fully control the motion of any graphic object in any animation scene, such techniques are also referred as motion specific techniques because we can specify the motion of any graphic object in scene, techniques like interpolation, approximation etc., are used in motion specification of any graphic object.
High level techniques (motion generalized)
Techniques used to describe general motion behavior of any graphic object, these techniques are algorithms or models used to generate a motion using a set of rules or constraints. The animator sets up the rules of the model, or chooses an appropriate algorithm, and selects initial values or boundary values.
Q Explain how acceleration is simulated in animation? Discuss all the cases ie zero acceleration, positive acceleration, negative acceleration and combination of positive and negative acceleration.
Ans Little mathematics is needed to describe simulation of acceleration in animation. As the motion may be uniform with acceleration to be zero, positive or negative or non-uniform, the combination of such motions in an animation contributes to realism. To impart motion to a graphic object, curve fittings are often used for specifying the animation paths between key frames. Given the vertex positions at the key frame, we can fit the positions with linear or non-linear paths, which determines the trajectories for the in-between and to simulate accelerations, we can adjust the time spacing for the in-betweens.
Different ways of simulating motion are listed below:
Zero Acceleration (Constant Speed)
Negative accelerations or Decelerations
Combination of accelerations
Zero Acceleration (Constant Speed): Here, the time spacing for the in-betweens (i.e., in-between frames) is at equal interval; i.e., if, we want N in-betweens for key frames at time Ta and Tb, then, the time interval between key frames is divided into N+1 sub-intervals leading to in-between spacing of Δ T given by the expression
Note: A linear curve leads to zero acceleration animation.
Non-Zero Accelerations: This technique of simulating the motion is quite useful introducing the realistic displays of speed changes, specifically at the starting and completion of motion sequence. To model the start-up and slow-down portions of an animation path, we use splines or trigonometric functions (note: trigonometric functions are more commonly used in animation packages, whereas parabolic and cubic functions are used in acceleration modeling).
- Positive Accelerations: In order to incorporate increasing speed in an animation the time spacing between the frames should increase, so that greater change in the position occur, as the object moves faster. In general, the trigonometric function used to have increased interval size the function is (1-Cos Θ) ,0<Θ<Π/2 .
Negative Accelerations: In order to incorporate decreasing speed in an animation the time spacing between the frames should decrease, so that there exist lesser change in the position as the object moves. In general, the trigonometric function used to have increased interval size the function is Sin Θ ,0<Θ<Π/2.
Combination of Positive and Negative accelerations: In reality, it is not that a body once accelerated or decelerated will remain so, but the motion may contain both speed-ups and slow-downs. We can model a combination of accelerating – decelerating motion by first increasing the in-between spacing and then decreasing the same.
Δ T=time difference between two keyframes =Tb-Ta
Q What is windowing transformation? Discuss the real life example where we can apply the windowing transformation?
Ans Let us first understand the terms window and viewport before knowing windowing transformation as a whole.
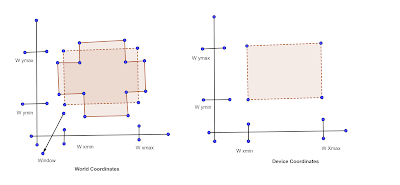
Window: A world coordinate area selected for display (i.e. area of picture selected for viewing).
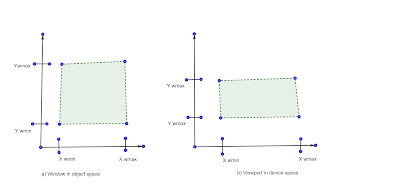
Viewport: An Area or a display device to which a window is mapped.
- Window defines what is to be viewed and viewpoint defines where it is to be displayed.
- Often window and viewpoints are rectangles in standard position with edges parallel to coordinate axes. Generalised shapes like polygon etc., take long to process, so we are not considering these cases where window or viewport can have general polygon shape or circular shape. The mapping of a part of a world coordinate scene to device coordinates is referred to as Viewing Transformation. In general 2D viewing transformations are referred to as window to viewport transformation or windowing transformation.
Q Write and explain the pseudocode for Sutherland Hodgman polygon clipping algorithm.



